matura TOmek: Jak tam rozszerzenie z majmy Jakie zadanka, jakie odczucia?

romanooo: że tak powiem, mam nadzieję że fizą nadrobię

TOmek: była wartosc bezwzględna?

romanooo: nie....

TOmek: to super, bedzie z rok

TOmek: za*

romanooo: Uzasadnij jeśli P(A)= 0,9 P(B)= 0,7 że P(A⋀B') ≤ 0,3

luk18: No własnie, jest ktoś, kto pokazałby jak zrobić to zadanie co romanoo napisał? Było 12 zadań, I same na udowodnij, uzasadnij.... Tylko jedno było z parametrem przyjemne zadanie

Maciuś: luki18 czyli jednym slowem porażka?

LOL: robie

Kejt: dobrze, że piszę za dwa lata

Maciuś: Mowisz że same udowodnij? heh dobrze że nie zapisywalem roz. bo bym tylko stracil czas

Vax: Fajnie, że dają do wykazania dowody, dowód to podstawowa rzecz w matematyce, jak to kiedyś powiedział Przemysław Mazur

luk18: Powiem tak, co nienawidzę zadań z udowodnij, uzasadnij to zrobiłem wszystko.... Sam się sobie dziwię, ale czy dobrze to pewności nie mam.... Naprawdę w tym roku rozszerzenie było kosmiczne

Maciuś: Powiem wam ze dobrze, że podniesli poziom z matur tylko mogli uprzedzic troche wczesneij np trudniejsza probna wg mnie jedyna probna matura od CKE to byl banal ,a przewaznie probna byla trudniejsza od oficialnej

Kejt: ciekawe jak Godziowi poszło..

Maciuś: Vax Tu sie z Toba zgodze w 100% tymi zadaniami ukazuja sie ludzie ktorzy znaja matematyka ,a nie umią . To zasadnicza roznica znac a umiec. Ci ktorzy zdaja roz maja wyuczone zdadania i licza na podobne u wg schematu podążaja . Osoby ktorzy ogarniaja matme , rozumia i dzialaja

romanooo: no pojechali z tą próbną... próbna taka banalna, a teraz przyjebali... to co było w zeszłym roku przy dzisiejszej to jak podstawa...

Kejt: umieją..nie umią

Wojteq66: jak dla mnie rozsezrzenie trudne było...

Godzio: Kejt ... "Ciekawe jak Godziowi poszło" − chyba nie za fajnie ... liczę na 94 − 98%

Piotrek: Czy komuś wyszły paskudne wyniki w zadaniach o środkowej i o sinusie w ostrosłupie?

luk18:

Alfred PRO: P(A)= 0,9 P(B)= 0,7 mam udowodnic ,ze P(A⋀B') ≤ 0,3 P(A⋀B)=0,9−0,7=0,2 P(B')=1−P(B)=0,3 P(A⋀B')=0,9−0,2=0,7 Na pewno dobrze przepisałes dane z tego zadania?

TOmek: jak ktos bedzie miał arkusz odrazu dawać link

luk18: Mi wyszły paskudne, sinα=U{2√82{41} a o środkowej to chyba 2√42

romanooo: mi teżż tak wyszedł sinus

luk18:

	2√82
sinα=
	41

Tomek.Noah: Alfred napewno tak nie bedzie a luk mi sin tyle samo wyszedl ale srodkowa inaczej...

rumpek: Świeżutkie http://www.cke.edu.pl/images/stories/00002011_matura/R/pr_matematyka.pdf dopiero wrzucili

romanooo: środkowa też

luk18: No to super może jakieś punkty dostane

Piotrek: luk18: mam podobnie, ale nie wiem czy identycznie także coś w tym jest

TOmek: rumpek danke xD

rumpek: Zadanie 1 k⁶ − 2k⁴ + k² = k²(k⁴ − 2k² + 1) = k²(k² − 1)² = k²(k − 1)²(k−1)² = [k(k−1)(k+1)]² Widzimy, że są to 3 kolejne liczby całkowite w których przynajmniej jedna jest parzysta oraz jedna podzielna przez 3. Iloczyn takich liczb dzieli się przez 2 * 3 = 6. Więc k(k−1)(k+1) dzieli się przez 6, zatem [k(k−1)(k+1)]² dzieli się przez 36 c.n.u.

TOmek: ale dali zadanie z ciągów , omg

luk18: No nieźle Ale zadanie... No niestety tak go nie zrobiłem...

rumpek: Ciekawe zadania

Wojteq66: http://i1.kwejk.pl/site_media/obrazki/70425-wykradziona-matura-2011.jpg

Wojteq66: 4 dowody w 1 arkuszu

Ktuś: Jak zrobić to zadanie Dany jest czworokąt wypukły ABCD niebędący równoległobokiem. Punkty M, N są odpowiednio środkami boków AB i CD. Punkty P, Q są odpowiednio środkami przekątnych AC i BD. Uzasadnij, że MQ || PN .

rumpek: W zadaniu 3 należało pamiętać o: Δ > 0 x₁ * x₂ < 0 x₁ + x₂ > 0 i zauważyć: (x₁ − x₂)² = x₁² − 2x₁x₂ + x₂² = x₁² + x₂² − 2x₁x₂ = (x₁ + x₂)² − 4x₁x₂

romanooo: jest ktoś chętny policzyć całość

luk18: Też jestem ciekaw rozwiązania

Tomek.Noah: z ciagiem to ja akurat zrobilem dobrze

TOmek: zadanie 2 . c={a+b}{2}

a		b		a+b
	+		=2 /*a−
a+b   a−   2		a+b   a−   2		2

	a+b
a+b=2*(a−		)
	2

a+b=2a−a+b a+b=a+b dobrze?

K+K: dokładnie już mogę sobie pomarzyć że to zdałam a tak mi zależało

fefd: niby czemu rumpek te założenia ? nie bylo podane 2 pierwiastki róznych znaków

Wojteq66: w m mi wyszło jakoś m nalezy (0,1) suma (2,3)

wolfy: w 3 mi wyszlo m∊(0,1)∪(2,3) albo cos kolo tego...

TOmek: nie nawidze zadań , "uzasadnij"

luk18: Mi tyle co Wojteq66 i zgadzam sie z fefd

TOmek: nie nawidze zadań , "uzasadnij"

Kosmos: Kosmos tyle powiem

rumpek: Racja moja wina nie doczytałem w takim razie Δ > 0

Vax: @Ktuś, można to szybko udowodnić w ten sposób, połóżmy na to płaszczyznę zespoloną i przyjmijmy odpowiednie współrzędne zespolone:

	a+b		c+d		a+c		b+d
A(a) , B(b) , C(c) , D(d) , M(		) , N(		) , P(		) , Q(		)
	2		2		2		2

	a−d		a−d		1
Teraz zauważ, że (M−Q)x(P−N) = (		)x(		) =		(a−d)x(a−d) = 0 co dowodzi
	2		2		4

tego, że MQ jest równoległe do PN. Pozdrawiam.

Tomek.Noah: wychodzilo tak ze m∊(−1,1)∪(2,+∞) m∊(−∞,−1)∪(0,3) wiec wychodzi chyba (2,3) tak wiekszosc w kalsie miala

Wojteq66: a ile rozwiazan w rownaniu tryg.wam wyszlo ? mi chyba aż 6...pewnie zrąbałem cos..

wolfy: 1 raz slysze o tych plaszczyznach

Tomek.Noah: z tym co Vax pisze udowodnic mozna bylo w kierunku w tym ze to jest rowneleglobok ...

Godzio: (0,1) U (2,3) Tomek.Noah

rumpek: Rzeźnicze te zadania dwa ze stereometrii, 4 dowody Żeby za rok dali łatwiejsze. Teraz pewnie takie dali bo rok temu za dobrze poszło

Tomek.Noah: ja nie pamietam ale tez duzo ich bylo4 cos takiego...

K+K: to właśnie nie miał być równoległobok wyraźnie było zaznaczone

wolfy: HA @Tomek.Noah na pewno dobrze jest gdy to jest rownoleglobok? zrobilem tak

Vax: Dokładnie, trzeba było udowodnić dla czworokąta niebędącego równoległobokiem

Tomek.Noah: Godzio (2,3)

Tomek.Noah: ale ten maly byl nie duzy...

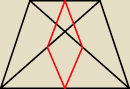
wolfy: K+K o to mi chodzi...

kamil: porażka, rozszerzenie lepiej mi poszlo mysle o 90−95 % a podstawa, nie wiem dlaczego byla dosyć trudna... bede mial ok 80%

Tomek.Noah: fuck ja pierdziele zle odczytalem zbior m...

K+K: aaaaaa.....

Vizer: mi tez wyszlo (2,3) xD

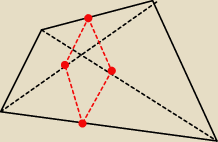
Tomek.Noah: i ten czerwony po wyliczeniach jest rownoleglobokiem

Godzio: A ja sobie narysowałem wszystko na osi, i odczytałem elegancko

Vax: E tam, na zespolonych najszybciej wychodzi

asdfg: kąt od tych stycznych wyszedł 90 stopni?

wolfy: Godzio wiec jak bylo poprawnie? sa jakies odp bo google nc nie wie :<

Tomek.Noah: Jestem zmieszany po tej maturze (rozszerzonej...)

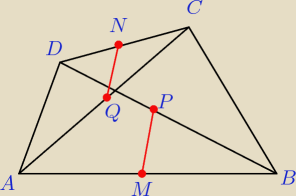
Godzio: Ja skorzystałem z tw. o odcinku łączącym środki dwóch boków trójkąta: PM || AD NQ || AD PM || NQ Co należało wykazać, tylko oczywiście nieco się rozpisałem żeby się nie przyczepili

Piotrek: asdfg: mi wyszedł 90

Tomek.Noah: tak

Tomek.Noah: ja tak samo Godzio

rumpek: 2sin²x − 2sin² xcos x = 1− cos x 2 * (1 − cos²x) − 2(1 − cos²x)cox = 1 − cosx 2 − 2cos²x − (2 − 2cos²x)cosx = 1 − cosx 2 − 2cos²x − (2cosx − 2cos³x) = 1 − cosx 2 − 2cos²x − 2cosx + 2cos³x = 1 − cosx 2cos³x − 2cos²x − cosx + 1 = 0 2cos²(cosx − 1) − 1(cosx − 1) = 0 (cosx − 1)(2cos²x − 1) = 0 (cosx − 1)(√2cosx − 1)(√2cosx + 1) = 0 I teraz odczytujemy, tak Godzio ?

Godzio: Można tak, ale łatwiej: 2sin²x − 2sin²xcosx = 1 − cosx 2sin²x(1 − cosx) = 1 − cosx 1 − cosx − 2sin²x(1 − cosx) = 0 (1 − cosx)(1 − 2sin²x) = 0 (1 − cosx) * cos2x = 0 cosx = 1 lub cos2x = 0 I teraz można odczytywać

wolfy:

	π		3π		5π		7π
rumpek tez tak robilem wyszlo 6 wynikow 0,2π,		,		,		,
	4		4		4		4

Godzio: wolfy mam identycznie

Kuba: też tak mam, f yea !

Kuba: A ile liczb 8 cyfrowych?

wolfy: no moze 50% bedzie tylko ciagow nie zrobilem reszta jeszcze nie wiem

luk18: Kurde... a ja podzieliłem to obustronnie przez 1−cosx... i mam tylko trzy wyniki.... a szkoda... takie łatwe zadanie.

wolfy: kuba ja obliczylem ze ponad 8milionow xD

luk18: właśnie, ile tych liczb?

luk18: mi tez wychodziły jakieś kosmiczne ale stwierdziłem że nie moze aż taki wynik wyjść

Piotrek: Kuba: wg mnie C²₈ * C³₆ * W³₇

jan: mi wyszło coś koło 400

wolfy: ogolnie jest 89 999 999 liczb 8 cyfrowych wiec chyba dobrze...

stokrotka: mi tez wyszlo 6wynikow..ale ja mialam i dla sinx i dla cosx. wiec nie wiem czy to bd ok.

asdfg: a powiedzcie mi w tym zadaniu z graniastosłupem prawidlowym co trzeba było obliczyc najmniejsze pole , ile wyszło?

Grześ1992: a tak nei mozna bylo? 2sin²(1−cosx)=1−cosx / :1−cosx 1−2sin²x=0 cos2x=0 .............?

Godzio: Nie, bo pomijasz wynik

Tragos: to z graniastosłupem mi wyszło krawędź podstawy = 1

Grześ1992: kurcze może chociaż wtedy 2 pkt. za to dadzą

Kuba: mnie wysło około 80 tys tych liczb no cóż bywa A pierwsze wystarczy słowne uzasadnienie że iloczyn 3ech kolejnych liczb C jest podzielny przez 6 więc jego kwadrat jest podzielny przez 36?

luk18: a mam pytanie jak to z tym kątem i stycznymi, jak to policzyć, bo nie wiedziałem więc zrobiłem rysunek i z rysunku odczytałem współrzędne tych prostych i napisałem że ten kąt ma 90⁰

Vizer: grześ nie może być gubisz wyniki.

asdfg: kąt 90 stopni i krawędź 1 w graniastoslupie , Dobrze mam! yea !

Piotrek: liczysz proste i widzisz że a₁ * a₂ = −1 więc są prostopadłe

stokrotka: mi tez wyszedl 90stopni..

Tragos: luk tak 90 stopni wychodzi, ja sobie wyznaczyłem równania obu stycznych, a potem wzór na tangens kąta pomiędzy dwoma prostymi (z tablic), no i mianownik wychodził 0 − czyli tanges nie istnieje, więc kąt = 90

Vizer: Mnie wyszło 192080 takich liczb osmiocyfrowych

rumpek: Godziu myślę, że ta matura była trudniejsza, niż niektóre próbne matury zadania.info

Piotrek: Vizer: mi też

adam666: mi tez Viser

Vizer:

	8 3		6 2
I tak jest dobrze bo wychodzi coas takiego		*		*73

adam666: Zgadza sie, mi tez tak wyszło. Ale sam matura to hardcorowa. Nie dośćże czlowiek zmęczony po podst to jeszcze jakis zaprzeproszeniem **uj ułoży takie coś.

Rivi: w trygonometrii było 6 rozwiązań, jak ktoś pisał 0, 2, 1/4 3/4 5/4 7/4 (pi wszystko)

Tragos: a no ja kur** wziąłem głupi na końcu *9³... ja pier

Kuba: Ale szczerze uważacie że była trudna? Ja jestem z klasy językowej, opierdalałem się a nie przygotowywałem i pierwsze 6 zadań, spokojnie potem już ciężko ale spodziewałem się czegoś trudniejszego...

luk18:

	6 2		8 2
A ja wziąłem zamist		mam

stokrotka: to moze rozpisz te pierwsze 6 zadan : ) bo na oko one moga sie nie wydawac trudne.. albo jestes taki dobry . jednak wiekszosc uwaza,ze to nie byla latwa matura i w takim razie wiekszosci sprawila kłopot.

stokrotka: chyba,ze pisales to zwracam honor i gratuluje

Tomek.Noah: Ja prawdopodobienstwo spieprzylem ale jak patrze na wyniki na innych forach jest zle wrecz dobrze

Tomek.Noah: *nie jest

Patryks: teraz patrze na wyniki i z podstawy bede miał około 92−94 % a rozszerzenie to masakara... Jak bedzie 70 % to bedzie cud...

wolfy: Patryks mam podobnie

Tomek.Noah: ja podstawowa 98−100 a rozszerzona to nie weim ale od 75% w gore

wolfy: w zadaniu 6 ile wam wyszla AD?

stokrotka: pewnie wieczorem bd gdzies rozwiazane te zadania na necie to sobie sprawdzimy

Piotrek: wolfy: coś z √21

gawi: ja pitole masakra byłaq takie głupie błedy zrobiłam że ała a powiedzcie mi z tym ostrosłupem jak wyszło i ile środkowa wyszła

tom: Bez wątpienia tegoroczna matura była o wiele bardziej trudna niż zeszłoroczna lub ta sprzed 2 lat. Niby zakres materiału ten sam ale zadania o wiele bardziej nietypowe i zwyczajnie trudniejsze. Zeszłoroczni maturzyści mieli nieporównywalnie łatwiej i możemy im tylko teraz zazdrościć Niech jeszcze jutro nie będzie rozprawki na angielskim to też będzie pięknie..

gawi: aaa i prosze o przeanalizowanie 8 bo nie wiem czy dobrze zrobiłam

wolfy: mi wyszla 4 chyba <haha>

wolfy: tom lepiej ze byla trudniejsza beda mniejsze progi

Piotrek: a jak liczyłeś?

Rivi:

	√46
Mi sinus w ostrosłupie wyszedł		}..
	8

wolfy: obliczylem ramie pozniej obliczylem pole trojkata poznej porownalem pole trojkata z innym... ale widze ze bedzie to zle ...

Patryks: Mi AD wyszło 4

Tragos: ja ramię liczyłem, a potem tw. cos, no też mi nie za ładny wynik tam wyszedł

Piotrek: Ja przyjąłem że środkowa dzieli trójkąt na 2 równe pola i z tych 2 trójkątów policzyłem ramię i dalej z tw. cosinusów

Rivi:

8. 12a+6b=24 ⇔ 2a+b=4 a∊(0,2)

Pb=6*a*b=6a(4−2a)=−12a²+24a f(a)=−12a²+24a funkcja maleje blablabla największe pole w wierzchołku a_w=1

gawi: Nooo mi 4 nie wyszło mi 4 pierwiastki cos tam na 3 chyba

Tomek.Noah: Rivi tak samo

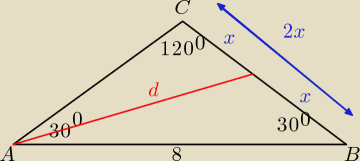
rumpek: Zadanie 6 Najpierw wyjdę od twierdzenia sinusów:

8		2x
	=
sin120o		sin30o

sin120^o: sin(180^o − α) = sinα

	√3
sin(180o − 60o) = sin60o =
	2

8		2x
	=
√3     2		1   2

Mnożę na krzyż i otrzymuję:

	√3
4 = 2x *
	2

√3x = 4 / : (√3)

	4		√3		4√3
x =		*		=
	√3		√3		3

Jak mam wyliczone x to dalej już tylko korzystam z twierdzenia cosinusów.

	4√3		4√3
d2 = (8)2 + (		)2 − 2 *		* 8 * cos30o
	3		3

	16 * 3		32√3		√3
d2 = 64 +		− 2 *		*
	9		3		2

	48		32 * 3
d2 = 64 +		− 2 *
	9		6

	48		96
d2 = 64 +		−
	9		3

	192		16		96
d2 =		+		−
	3		3		3

	208		96
d2 =		−
	3		3

	112
d2 =
	3

	112		112
d = √		v d = −√		∉ N+
	3		3

Chyba coś pomieszałem, nie ?

Kosmos: ale trudno to liczyłeś ja odrazu z twierdzenia cosinusów

Kosmos: a jednak tak samo liczyłęm

Piotrek: rumpek: widzę znajome wyniki

tom: wolfy dla kogos kto zdawal w tamtym roku ale nie dostal sie gdzies tam sytuacja jest wymarzona, bo progi poleca, ale tegorocznym w zaden sposob nie zmienia sytuacji mniejsze progi ale generalnie mniej punkow tez. Moze byc wrecz gorzej, jesli duzo osob z zeszlego roku ponownie bedzie ubiegac sie o przyjecie

rumpek: Tylko gdzie się "dupnąłem"

Kosmos: matura rozszerzona mnie załtwiła mam nauczkę że by się więcej uczyć matematyki

luk18: A czy mógłby ktos 2 ostatnie zadania zrobić?

Kosmos: wolfy ty piszesz drugi raz maturę ?

Rivi: Mi x wyszedł taki sam, długości tego badziewia już nie pamiętam... (x można z pitagorasa xD ja z cosinusów robiłem )

Kosmos: myśle że 60% będzie w sumie to mi styka

rumpek: Zadanie 7 x² + y² + 2x − 2y − 3 = 0 x² + 2x + 1 + y² − 2y + 1 − 1 = 0 (x + 1)² + (y − 1)² = 1 S = (−1,1) r = 1 Tak o ? jeszcze w szkole nie miałem ni twierdzenia sin/cos ani tych okręgów

Tomek.Noah: (x+1)²+(y−1)²=5

Kosmos: no mi r też wyszło √5

rumpek: Chyba wiem dlaczego Tomek.Noah tak tobie wyszło muszę tylko doczytać o tych nieszczęsnych okręgach

rumpek: Pewnie moja wina teraz wiem skąd się to wzięło.

Wojteq66: r=√5 mi wyszlo i na tym poprzestalem, dodalem notke tylko ze dwie proste musza byc odlegle od srodka o √5

Rivi: 13. P(A/\B')=P(A\/B)−P(B) P(A\/B)≤1,6 wyszło z wzoru, ale max może być 1 więc P(A\/B)≤1

przekształcam to pierwsze na

P(A\/B)=P(A/\B')+P(B) 1≥P(A/\B')+P(B) 1≥P(A/\B')+0,7 P(A/\B')≤0,3

Vax:

	4√21
U mnie na szybkiego w zadaniu ze środkową trójkąta wychodzi		raczej ok.
	3

Wojteq66: ale teraz jak patrze... to było do zrobienia z tymi okregami cholera...

adam666: mam propozycje , może założymy nowy temat gdzie będą rozwiazania tych zadan? tylko zeby nikt tam nie spamował, by było widoczne, czarno na białym.

Artur: a mi wyszło 2√10

Artur: ze srodkową

wewe: na maturze mialem taki wynik chba jak Vax tutaj wyzej z ta srodkowa

rumpek: No Vax tobie wyszło tak jak Godziowi tylko gdzie ja się tam pomyliłem ?

Piotrek: Vax poprawiasz mi humor

Vizer:

	4√21		112
Ni chce nic mówić ale		=
	3		3

luk18: Nie rozumiem tego zadania 12..

Vizer:

	112
√
	3

luk18: A jaki wam sinus wyszedł w 11?

Vax: @rumpek, nigdzie się nie pomyliłeś

	112		√112		4√7		4√21
d2 =		⇒ d =		=		=
	3		√3		√3		3

Ujemne rozwiązanie odpada, ponieważ długość boku nie może być ujemna

rumpek: Szocke zapomniałem niewymierność wypierdzielić

Maturzysta: Panowie i Panie, moje czy grosze. Podoba mi się, że tegoroczna matura rozsz. stoi na tak wysokim poziomie. Problem w tym, że inaczej było w maturami poprzednimi. To po prostu niesprawiedliwe dla tegorocznych maturzystów "rozszerzonych".

gawi: No nie fer... kurde ja się serio dużo uczyłam i proszę dowalili takie zadania a te ciągi to już w ogóle o ale podstawe mam na 94% xD

Patt: No kosmos. Tragedia z leksza ta matura. Podstawa uważam, że była trudna dla humanisów. Ale rozszerzenie było straszne...

matura: w zeszłym roku za przyzwoity wynik można było uznać dopiero 80% i więcej, w tym myślę że jak ktoś kto napisał na 60% nie ma się czego wstydzić. Odbije się to pewnie na progach punktowych przy rekrutacji na studia. Niestety dla nas, tegorocznych maturzystów, to nie jest dobra informacja, ponieważ zeszłoroczni najprawdopodobniej wykoszą nam sporo miejsc, przez co progi w rzeczywistości nie spadną aż tak znacząco, a punktów z porównywalną czy czasem nawet większą wiedzą mamy mniej. eh, niestety cke pokrzyżowała wielu z nas plany, dając z roku na rok maturę o całkowicie innym poziomie trudności.

kamil: @matura pisałem w tym roku i w tamtym i ja OSOBIŚCIE uważam że w tym była łatwiejsza DLA MNIE

kubao: No niestety z rozsz bede mial pewnie tylko ok. 30−40%, dobrze ze podst mi fajnie poszla...

Maciuś: matura masz 100% racje . Nie ma i nie bedzie sprawiedliwosci na tym świecie

Tragos: a no co poradzicie.. zobaczymy co to będzie końcem czerwca, trzeba być dobrej myśli póki co ja spadam, coś na angielski trzeba luknąć

meg: Trudna była ... Nie było najprostszych zdań...np z wartosci wezwzglednej, wyznaczenia reszty wielomianiu itd:( szkoda...ale swiat sie nie zawalił moze cos tak sie wyskrobie punktów

Kosmos: e tam ale podstawa dobrze poszła to myślę na politechnike wystarczy

Alaila: co wam powiem to wam powiem: ponad 3 lata nie miałam styczności z matmą. pisałam dziś rozszerzoną. uczyłam się do niej sama. ok 40% będę mieć. poziom oceniam na prawdziwie rozszerzony. to już moje egzaminy na studiach (3 rok prawa) sa prostsze

KKK: Podstawa akurat nie była taka trudna jak w wiadomościach krzyczeli, natomiast rozszerzenie to tragiczne. Przerobiłem 6 arkuszy z Cewe rozszerzonej i w każdej miałem około 70%, natomiast z dzisiejszej matury pr. czuję, że będzie koło 30−40 %. Szkoda ale mam nadzieje, że dostanę się na PB. A jak nie to w sumie też nic się nie stanie, pójdę do roboty + korki pod rozszerzenie i za rok pizgne na 100% haha Pozdrawiam maturzystów !

essh: juebane cosinusy xD nie zdazylem tego porobic i Oo xD 4 pkt bye bye bo zrobilem tak jak ktos wyzej ze podzielilem przez ten 1−cosx z zalozeniem ze cosx nie moze byc rowny 1 xD aaa tammm xD ja sie pytam gdzie wielomiany i wartosc bezwzgledna xD

kubao: kkk w 100% mam taką samą sytuację, z próbnych miałem zawsze ok 50−70% tutaj na więcej niż 40% nie liczę...

Epo: Poprawiałem maturę w tym roku. I chyba w następnym będzie kolejna poprawka